【苦手な人向け】三角関数と単位円
「三角関数(三角比)が苦手。」という声はよく耳にします。
このページを見ていただいているということは、あなたも三角関数に苦戦しているのでしょう。
大学受験以外にも、意外と社会人になってからも使う機会が多い三角関数。
苦手なままではいられないあなたにとって、この記事が少しでも助けになれば幸いです。
三角関数の定義
そもそも、三角関数とは何だったかをおさらいしましょう。
.png)
Oを原点とする座標平面上で、点Xの座標を(r,0)、点Pを円 x2+y2=r2(r>0)上の動点とします。
また、半直線OXを始線としたときの動径OPまでの角度(反時計回り)をθとします。
このとき、点Pの座標を(x,y)として
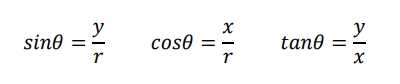
と定義しました。
これらを、θの三角関数といいます。
単位円で考える
定義を見ていただくと、文字式であることに加えて、分数も出てきていることがわかると思います。
僕は、定義が分数の形になっていることも、三角関数に苦手意識を持ってしまう一つの要因になっていると思います。
そこで、三角関数が苦手な方には、必ず意識してほしいことがあります。
それは、単位円(r=1の円)で考える、ということです。
こう言うと、「rをそんな都合いい数字で考えていいの?」と聞かれることもありますが、
三角関数は角度θに対応しているのであって、半径rの値には影響されないので問題ありません。
文章で説明されてもわからない方は、一緒に図をみて確認してみましょう。
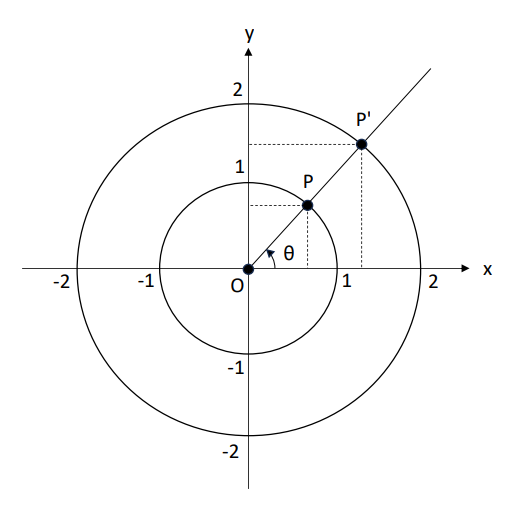
試しに、r=1の場合(単位円)とr=2の場合で、それぞれ三角関数を考えてみます。
まず、r=1の場合です。
r=1の円上にある点Pの座標を(x,y)、角度をθとしたとき、θの三角関数は次の通りになります。
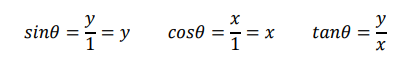
続いて、r=2の場合はどうでしょうか。
先ほどの点Pの座標が(x,y)であったため、r=2の円周上にある点P’の座標は(2x,2y)となります。
このとき、θの三角関数は次の通りになります。
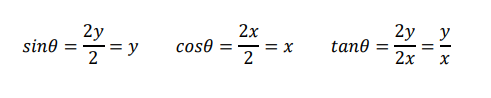
ご覧の通り、rの値が違っても、θが変わらなければ、θの三角関数も変わらないのです。
単位円で考えるわけ
そもそも、なぜ単位円で考えることを意識してほしいかというと、定義の分数がややこしいからだけではありません。
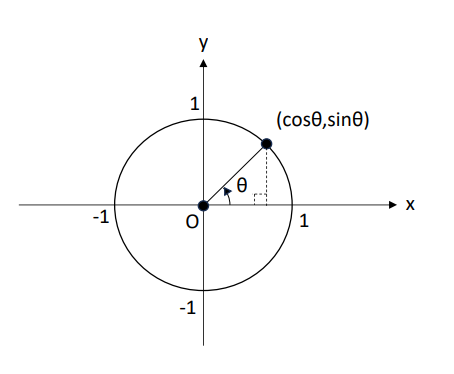
一番の理由は、単位円において点Pの座標(x,y)を(cosθ,sinθ)として見てほしいからです。
この見方が出来るようになれば、今後出てくる公式を理解するうえで必ず役に立ってくれるはずです。
(例えば、三角関数の相互関係 sin2θ+cos2θ=1 や、負角の公式 sin(-θ)=-sinθ などなど…)
おわり
人によっては、三角関数の定義を単位円で習ったという方も少なくないかもしれません。
そんな方々にとっては、何一つ新たな発見のない記事だったでしょう。
しかし、中には
「単位円って、聞き覚えはあるけど、結局何で話題に出てきたのかもわからない。」
という方も一定数いることから、この記事を書くに至りました。
そんな方々のテストの点数が、1点でも上がることを、僕は願っています。




